Leveraging enhanced egret swarm optimization algorithm and artificial intelligence-driven prompt strategies for portfolio selection

Abstract

In the financial field, constructing efficient investment portfolios is a focal point of research, encompassing asset selection and optimization of asset allocation. With the advancements in Large Language Models (LLMs), generative Artificial Intelligence (AI) tools have showcased capabilities never seen before. However, the black-box nature of these tools renders their outputs difficult to interpret directly, often necessitating iterative fine-tuning to align with users’ expected outcomes. This study presents a structured prompt framework specifically designed for stock selection, aiming to provide direct and interpretable stock-selecting tools for investors of various levels. By creating representative scenarios and combining them into different cases for experimentation, we can explore how the construction of prompts influences the responses generated by generative AI tools. Additionally, this paper proposes a novel algorithm that combines the Nonlinear-Activated Beetle Antennae Search strategy with the Egret Swarm Optimization Algorithm (NBESOA) to address the Mean-Variance Portfolio Selection problem with Transaction Costs and Cardinality Constraints (MVPS-TCCC), utilizing real stock market data to construct portfolios based on generative AI tools recommendations. Simulation results indicate that, compared to other algorithms, NBESOA prefers optimizing portfolio configurations to achieve the highest Sharpe Ratio with the strictest constraints, bringing the outcomes closer to the portfolio’s efficient frontier.

Introduction

As a significant milestone marking the entrance into a new era in the field of Artificial Intelligence (AI), Large Language Models (LLMs) have made breakthrough advancements in science and technology, greatly influencing the way humans develop and apply AI¹. Compared to early language models (LMs), the emergence of LLMs signifies a fundamental shift in the scientific thinking of current researchers². They have overcome the limitations of early LMs that could only model and generate text data, demonstrating powerful capabilities in solving a diverse range of complex tasks³. This phenomenon has propelled extensive scholarly discussion on the concept of Artificial General Intelligence (AGI)⁴. Natural Language Processing (NLP), as the cornerstone enabling the powerful capabilities of LLMs, has played a crucial role⁵. It allows LLMs to understand and generate language at a deeper level, thereby achieving highly natural human-computer interaction in a wide range of application scenarios⁶. Introducing LLMs with advanced NLP capabilities has initiated a revolutionary transformation in the financial field. This change is characterized by the integration of AI-driven insights into traditional financial practices, enhancing accuracy, efficiency, and personalized service delivery. LLMs are increasingly used to interpret complex financial reports⁷, analyze market sentiment from a vast array of news articles and social media data⁸, and predict market trends with greater precision. Therefore, financial enterprises are increasingly reliant on LLMs to quickly distill key insights from massive datasets⁹. With the proliferation of LLMs, tasks previously considered challenging are now feasible, further expanding the potential applications of AI in the financial domain^10,11.

In 2022, the release of ChatGPT by OpenAI sparked a wave of discussion in the field of LLMs¹². Since the initial introduction of the GPT architecture in 2018, OpenAI has continually expanded its training dataset, upgraded the technology, and improved the architecture, ultimately achieving the most advanced version to date, GPT-4¹³. ChatGPT, as a specialized version of the GPT architecture tailored for conversational applications, not only demonstrates the powerful capabilities of LLMs in understanding and generating natural language but also exhibits exceptional interactiveness and adaptability in practical applications¹⁴. This is attributed to its foundation as a pre-trained Transformer model, emphasizing dialogue management and context understanding¹⁵. Combined with NLP technology, it can handle various topics and tasks, thereby promoting the further application and development of NLP technology. In the financial domain, especially in portfolio management, creating high-quality inputs to obtain optimal responses has become a focus of research. The process of optimizing the prompt, defined as “prompt engineering”, aims to achieve desired outcomes through high-quality communication between users and LLMs^16,17. Prompt engineering is crucial for enhancing the interaction efficiency and output quality of LLMs, relying on precise question formulation, deep understanding of the target topic, and comprehensive mastery of LLMs’ operating principles and limitations¹⁸. Moreover, it involves a dynamic optimization process, continuously refining questioning strategies through experimentation, adjustments, and leveraging the diversity of model outputs¹⁹, thereby enhancing the model’s performance on specific tasks²⁰. The development of prompt engineering has effectively improved the precision of LLMs in generating investment strategies, providing new vitality for the development of portfolio management.

Bio-inspired algorithms, characterized by fewer parameter settings and faster optimization speeds, are widely applied to solve optimization problems^21,22,23. Their abilities to handle complex non-convex optimization problems without relying on gradient information have made these methods increasingly popular in the field of portfolio investment²⁴. The Beetle Antennae Search (BAS) algorithm is a single-particle optimization algorithm that has received attention for its high computational efficiency and rapid convergence^25,26, making it extensively studied for optimizing investment portfolio problems^27,28,29. Besides single-particle algorithms like BAS, there are other swarm optimization algorithms inspired by collective behaviour, such as Genetic Algorithms (GA)^30,31, Particle Swarm Optimization (PSO) Algorithm^32,33, and Artificial Bee Colony (ABC) Algorithm^34,35 et al., which also demonstrate robust optimization capabilities in portfolio problems³⁶. In 2022, Chen et al. proposed a swarm intelligence optimization algorithm named Egret Swarm Optimization Algorithm (ESOA)³⁷. Compared to other swarm intelligence optimization algorithms, ESOA incorporates two different search strategies and adopts a learnable hyperplane estimation parameter, enhancing the algorithm’s interpretability and reducing computational complexity. This structured approach enables ESOA to effectively balance exploration and exploitation phases in optimization tasks and it has been widely applied in various fields such as healthcare^38,39, energy management⁴⁰, electrical systems⁴¹, and fraud detection⁴². This paper will employ a variant of the BAS algorithm to improve ESOA and apply it to constrained portfolio problems. The main contributions of this paper include:

(1) This paper presents a novel ChatGPT prompt framework for portfolio stock selection, generating effective investment advice without needing user-provided expertise, such as financial data. The advantage of this approach lies in its ability to offer applicable investment strategies to a broad user base, including non-professional investors, thereby expanding the audience for investment advisory services.

(2) Addressing complex factors in portfolio management, such as transaction costs and cardinality constraints, this paper transfers the multi-constraint optimization problem to multi-objective optimization and introduces penalty functions to construct the objective function. It proposes a Nonlinear Activated Beetle Antennae Search Improving Egret Swarm Optimization Algorithm (NBESOA) for optimizing stock asset allocation. Through comparative analysis with existing algorithms, it confirms its effectiveness and superiority in solving practical engineering problems.

(3) The paper explores the specific impact of the proposed ChatGPT prompt framework on stock recommendation, providing users with a more convenient and explanatory method for obtaining investment recommendations through ChatGPT. Additionally, the integration of improving the ESOA algorithm to solve the MVPS-TCCC problem with stocks recommended by ChatGPT offers a new perspective to promote the application and research of artificial intelligence within the field of financial engineering.

The rest of this paper is organized as follows. “General frame of ChatGPT prompt for stock selection” analyzes the characteristics of effective prompts and proposes a general framework for LLMs prompts that incorporates the specifics of stock selection. In “Mean-variance portfolio selection considering transaction costs and cardinality constraints (MVPS-TCCC) problem”, a theoretical analysis of the PS-TCCC problem is conducted, and a loss function is constructed. “Nonlinear activated beetle antennae search improving Egret swarm optimization algorithm” introduces an improved version of the ESOA algorithm and tests its convergence performance on benchmark functions. “Experiments and discussion” is dedicated to designing experiments around the proposed prompt framework, aimed at investigating how it influences ChatGPT’s stock recommendations. Moreover, the PS-TCCC problem is optimized and validated using the NBESOA with real stock data. Finally, “Conclusion” summarizes the contents of this paper.

General frame of ChatGPT prompt for stock selection

In this section, a general prompt framework for LLMs is presented, designed to deliver clear and straightforward stock selection guidance to both non-professional and professional financial investors. Initially, the key traits of prompts that successfully lead LLMs to produce desired responses across diverse applications are summarized. This is followed by an analysis of stock selection strategies, with a focus on identifying features that align with ChatGPT’s capabilities. Finally, a general LLMs prompt framework is proposed for facilitating stock selection. Tailoring this framework to specific needs can enable investors to receive more personalized and relevant stock selection advice.

Fundamentals of prompt engineering

With the continuous development of LMs, prompt engineering has become an increasingly important skill. The core of this skill lies in designing refined prompts and continuously optimizing them to ensure that the input most accurately reflects the user’s intent, thereby obtaining the best response. As the sole method of interaction between the user and the model, the quality of the prompt directly influences the quality of the generated response. Effective prompts should possess the following characteristics:

• 1. Clear and easy to understand: The prompts should be clear, direct, and free from ambiguity or multiple interpretations. An effective prompt enables the model to accurately grasp the needs of users, thereby yielding more relevant responses.

• 2. Targeted towards a specific field: Effective prompts should be specific to a particular topic or field. By providing detailed information relevant to a specific subject, they help the model better understand the context and generate more professional and accurate responses.

• 3. Appropriate constraints: Overly broad prompts may lead to vague responses from the model, while overly strict constraints may limit the creativity and flexibility of the model. Therefore, when designing prompts, it’s important to find a balance between specificity and flexibility. Appropriate constraints can help the model focus on the actual needs of the users while maintaining enough flexibility to generate rich and creative content.

Table 1 presents examples contrasting bad and effective prompts. It can be seen that bad prompts are typically vague, misleading, and inappropriate, whereas effective prompts are clearer and more precisely defined, exhibiting specific constraints.

Table 1 Examples of poor prompt and effective prompt.

Table 2 Different type of prompts.

Therefore, a thorough study of prompt engineering is not only key to improving the effectiveness of model responses but also a crucial approach to achieving this goal. In the field of LLMs, research on prompt engineering continues to evolve, developing different types of prompts that can further enhance users’ understanding of creating effective prompts. Specifically, the format of prompts can be divided into Zero-Shot prompt, Few-Shot prompt, Iterative prompt and Structed prompt, which are shown in Table 2. It is noteworthy that compared to other types of prompts, iterative prompts and structured prompts stand out in fulfilling the characteristics of effective prompts. For generative AI, both iterative and structured prompts are effective means for fine-tuning. In stock selection, structured prompts may be more convenient for investors at different levels, as they offer a clear framework of information, facilitating the swift and accurate provision and reception of information.

The analysis of the efficiency and utility of the prompts provides detailed strategies and practical guidance for the construction of a general prompt framework for stock selection. This not only enhances the accuracy and efficiency of interactions with language models but also lays a solid foundation for investors to make more precise and personalized investment decisions in the complex stock market environment.

Improved framework for stock-selecting prompt

In the modern economic system, companies serve as foundational operational units and are key drivers of technological innovation and economic growth. Once a company has established a robust business model and achieved a certain scale, undertaking an Initial Public Offering (IPO) becomes a critical step in its development path. The IPO mechanism allows company shareholders to trade stocks on the public market, which is crucial for enterprises in scaling up their operations, funding research and development initiatives, managing debt repayment, and other related activities. In this process, the role of investors is indispensable. They provide substantial capital to companies through the purchase of stocks while also expecting to earn returns from these investments. Once investors buy into a company’s stock, their wealth becomes closely tied to the performance of the company, implying that they not only enjoy the profits from the company’s growth but also bear the corresponding risks. Therefore, in the investment decision-making process, investors must conduct a comprehensive and in-depth analysis of the company to make an accurate and professional assessment of its investment value.

Investors typically analyze the performance of companies from two perspectives: quantitative and qualitative. Quantitative analysis, based on numerical data, focuses on assessing a company’s financial health, profitability, growth potential, and risk level in stock selection. This analysis often involves a deep dive into the company’s financial statements, such as income statements, balance sheets, and cash flow statements, and adopting various financial ratios and indicators to evaluate the company’s operational efficiency and financial stability. Qualitative analysis concentrates on the company’s non-numerical factors, such as the quality of the management team, brand value, and corporate culture, to assess its long-term growth potential and competitive advantage. This type of analysis reveals information beyond financial metrics, such as innovation capabilities and customer loyalty, which significantly impact the company’s future performance. Although not easily quantifiable, qualitative analysis is crucial for assessing a company’s long-term value and risk. Experienced investors often combine quantitative and qualitative analyses to evaluate a company, gaining a comprehensive investment perspective.

In this paper, we consider using a representative LLM, ChatGPT, for stock selection from a non-quantitative analysis perspective. The main reasons are as follows:

• 1. Although ChatGPT is capable of handling specific financial data, its ability for large-scale financial analysis has limitations. When ChatGPT carries out complex quantitative analyses, such as in-depth financial ratio analysis and financial forecasting, it may not be as effective as professional financial analysis software.

• 2. Based on training in the vast array of textual data, ChatGPT excels in processing and interpreting language information. As a Text to Text (T2T) model, it is more suited for non-financial data analysis, such as assessing the quality of a company’s management, corporate culture, brand influence, and market trends. ChatGPT can integrate various complex qualitative factors, identifying connections between them, which helps investors understand non-financial factors that may affect stock performance.

• 3. The stock selection framework based on ChatGPT proposed in this paper is designed to be accessible to a wide range of users, including non-professional investors. Analyzing the patterns of stock selection through prompts can provide a theoretical basis for financial investors of all levels when using ChatGPT for stock selection.

In the process of financial investment decision-making, investors’ choices and actions are influenced by a variety of factors. Research in behavioral finance has uncovered the psychological and behavioral characteristics that affect investment intentions and decisions. According to the study by⁴³, the principal factors influencing investment decisions include individual factors, social influences, market information, company characteristics, product features, and demographic traits. It is evident that, besides personal factors, ChatGPT’s support in the investment decision process primarily stems from its extensive and fact-based pre-trained knowledge base. Therefore, in designing prompts for stock selection, it is crucial to focus on reflecting the individual factors of investors, which are listed in Fig. 1.

Figure 1

Diagram of investors’ individual factors that influence investment decisions.

In Fig. 1, all the factors considered, except for knowledge and experience, which are subjective factors derived from an investor’s capabilities, are objective factors that influence the investment process. The advantage of subjective factors is that they can directly affect the investor’s ability to identify investment opportunities, assess risks, select appropriate investment tools, and formulate effective investment strategies, playing a crucial role throughout the investment process.

Based on the above analysis, we propose a structured framework for using ChatGPT in the stock selection problem, which is defined as

$$\begin{aligned} \text {Prompt: } \left\{ \text {Strategy}\right\} \left\{ \text {Goal}\right\} \left\{ \text {Constraint*}\right\} . \end{aligned}$$

(1)

In this framework, “Strategy” refers to the basic guidelines taken in the stock selection process, “Goal” represents the investment objectives investors aim to achieve with the set of stocks selected by ChatGPT, and “Constraints” refers to additional restrictions investors wish to impose based on their individual needs, beyond the basic stock selection strategy. Additionally, the symbol “*” indicates that the “Constraint” element is optional when designing a prompt. This means that an effective response can still be obtained based on the settings of “Strategy”, even without specifying any constraints.

Subsequently, comparative experiments will be designed for each key component of the framework, aimed at validating its effectiveness and exploring its operational mechanisms in depth. Furthermore, it will be shown how the stock portfolio selected based on this framework can be effectively integrated into the investment portfolio optimization problem, thereby bridging theoretical concepts and practical application.

Mean-variance portfolio selection considering transaction costs and cardinality constraints (MVPS-TCCC) problem

In this section, the fundamental principles of the mean-variance portfolio selection (MVPS) problem are presented. Subsequently, we consider elements such as transaction costs and cardinality constraints that impact the model. Ultimately, for the sake of simplicity, these constraints are converted into penalties within the MVPS-TCCC model.

Definition of MVPS problem

It is assumed that the investor selects a set of N stocks from the stock market as the target for the portfolio, denoted as $\varvec{\Omega } = \{ \Omega _1, \Omega _2,..., \Omega _N \}$. The measurable space for this selection is represented as $(\varvec{\Omega }, \mathbb {F})$, where $\mathbb {F}(*)$ denotes the measurable function. The primary objective of the MVPS problem is the optimization of asset allocation and this is mathematically expressed as:

$$\begin{aligned} \mathcal {W} = \left\{ \varvec{w} \in \mathbb {R}^ {1 \times N}\Bigg | \sum _{n\in [N]}w_{n}=1, \; 0 \le w_{n} \le 1 \right\} , \end{aligned}$$

where $\mathcal {W}$ represents the set of weight allocations, with the constraint that the sum of all elements equals 1. It is also representable in matrix form as $\mathbf{{1}}{{\varvec{w}}}^\text {T} = 1$ and $\varvec{1} \in \mathbb {R}^{1 \times N}$ represents an all-ones vector. The weight $w_{n}$ constrained within [0, 1] is imposed to reflect the scenario where only stock purchasing (not selling) is considered.

For the time period $t \in [T]$, the return rate matrix for each asset in $\varvec{\Omega }$ is represented by $\tilde{\varvec{\mu }} \in \mathbb {R}^{T \times N}$. The mean return vector $\varvec{\xi }\in \mathbb {R}^{1 \times N}$ and the covariance matrix $\hat{\varvec{\Sigma }}\in \mathbb {R} ^{N \times N}$ for this MVPS problem are calculated as follows:

$$\begin{aligned} \varvec{\xi } = \frac{1}{T}{\sum _{t\in [T]} \tilde{\varvec{\mu }}_{t}}, \quad \hat{\varvec{\Sigma }} = \frac{1}{T-1} \sum _{t\in [T]} (\tilde{\varvec{\mu }}_{t} - \varvec{\xi })(\tilde{\varvec{\mu }}_{t} - \varvec{\xi })^\text {T}. \end{aligned}$$

It is noteworthy that the covariance matrix $\hat{\varvec{\Sigma }}$ is symmetric and non-negative, indicating that each element in position ij is equal to the element in position ji. In light of the established foundational knowledge, the MVPS problem can be mathematically structured as follows:

$$\begin{aligned} \begin{aligned}&\min _{\varvec{w}} \; \lambda \varvec{w} \hat{\varvec{\Sigma }} \varvec{w}^\text {T}- (1 - \lambda ) \varvec{w}{\varvec{\xi }}^\text {T}\\&{ \text{ s.t. }}\; \varvec{1} \varvec{w}^{\text {T}} = 1 \text {, } 0 \le \varvec{w}\le 1 \end{aligned} \end{aligned}$$

(2)

where $\lambda \in (0,1)$ is a tuning parameter within the interval (0, 1), balancing the trade-off between return and risk. This formulation is the basic Markowitz model, a fundamental tool in the financial industry for managing portfolios and evaluating risk.

The MVPS considering transaction costs and cardinality constraints (MVPS-TCCC)

While the Markowitz model offers a robust framework for the MVPS problem, practitioners such as investors and portfolio managers must also be cognizant of its underlying assumptions and potential limitations in real-world applications.

In MVPS problem, controlling transaction costs (including but not limited to commissions, market impact, slippage, and taxes) is of great importance. Asset allocation should be built based on the net returns post-transaction, i.e., the investment returns minus the transaction costs, and whether these align with the set investment objectives. Particularly in markets with low liquidity, large-scale trades can significantly affect transaction costs, leading to higher purchase costs or lower selling prices. In this paper, the transaction cost rate is assumed to be $\varvec{c} \in \mathbb {R}^{1 \times N}$. The total transaction costs incurred by the exchange of each stock $\Omega _i$ in the portfolio can be calculated as $\sum _{i=1}^{n}c_{i}w_{i}= \varvec{c} \varvec{w}^{\textrm{T}}$. Consequently, we modify the equality constraint in (2) to

$$\begin{aligned} \mathbf{{1}} \varvec{w}^{\textrm{T}} + \varvec{c} \varvec{w}^{\textrm{T}} = (\mathbf{{1}} + \varvec{c}) \varvec{w}^{\textrm{T}} = 1. \end{aligned}$$

(3)

This formula ensures that the total weight of the portfolio remains at some predetermined level (1 in this paper) after taking into account the transaction costs.

Furthermore, cardinality constraints also plays a crucial role in MVPS problem. Cardinality constraints directly limits the number of asset types in a portfolio, significantly impacting asset allocation and diversification strategies. It is commonly employed to comply with specific investment policies or regulatory requirements. Particularly in scenarios with high transaction costs or when investors have limited asset management capabilities, cardinality constraints assist in controlling transaction costs and maintaining the efficiency of portfolio management. Let $k \in [N]$ be the limit number of assets specified by the investor, the cardinality constraints can be mathematically imposed on MVPS problem as $\Vert \varvec{w} \Vert _0 = k$, where $\Vert \cdot \Vert _0$ is the $l_0$-norm that represents the number of non-zero entries in the vector. Corresponding to the cardinality constraints $\Vert \varvec{w} \Vert _0 = k$, a feasible set can be introduced:

$$\begin{aligned} \mathcal {Z}_N^k = \left\{ \varvec{z} \in \{0,1\}^ {1 \times N}\Bigg | \sum _{n\in [N]}z_{n}=k\right\} , \end{aligned}$$

(4)

where $\varvec{z} = [z_1, z_2,..., z_N]$ is a boolean vector containing only 0 or 1elements. $z_n = 0$ means that the nth asset in the portfolio is not selected by the investor, while $z_n=1$ means that it is selected. Then, the inequality constraint in (2) can be modified to

$$\begin{aligned} 0 \le w_n \le z_n. \end{aligned}$$

(5)

Therefore, the corresponding $w_n$ will change according to the value of $z_n$, i.e., when $z_n = 0$, $w_n = 0$.

When the MVPS problem considers (3) to (5), we can refine the description of the MVPS-TCCC problem

$$\begin{aligned} \begin{aligned}&\min _{\varvec{w}} \; \lambda \varvec{w} \hat{\varvec{\Sigma }} \varvec{w}^\text {T} - (1 - \lambda ) \varvec{w}{\varvec{\xi }}^\text {T}\\&{ \text{ s.t. }}\; ({\varvec{1}} + \varvec{c}) \varvec{w}^{\textrm{T}} = 1 \text {,} \; 0 \le w_n\le z_n\text {,} \; \varvec{z} \in \{0,1\}^ {1 \times N} \text {,} \; \mathbf{{1}} \varvec{z}^{\textrm{T}} = k. \end{aligned} \end{aligned}$$

(6)

Incorporating transaction costs and cardinality constraints makes portfolio optimization more representative of real-market scenarios. These constraints not only induce sparsity but also transform the optimization from simple linear or quadratic programming to a more intricate non-linear and non-convex combinatorial challenge. The MVPS-TCCC model offers a more precise depiction of the balance between risk and return, though it does increase the complexity of the resolution process.

Penalty parameters of MVPS-TCCC problem

In solving constrained optimization problems, adeptly managing constraints is crucial to discovering practical and viable solutions. An effective strategy is to reformulate constrained problems as unconstrained ones by integrating penalty constraints, thereby simplifying the resolution of nonconvex problems. In this paper, we convert the constraints specified in (6) into a series of penalty terms, aiming to reduce the complexity involved in addressing the nonconvex problem.

In addressing the constraints delineated in (6), streamlining the equality constraints can be achieved with a refined approach. This entails shifting the terms from the right to the left side of the equation, followed by elevating the transposed terms to a square power. Consequently, constraints such as $(\varvec{1} + \varvec{c})\varvec{w}^\text {T} = 1$ and $\varvec{1z}^\text {T} = k$ are respectively reformulated as

$$\begin{aligned} ((\varvec{1} + \varvec{c})\varvec{w}^\text {T} - 1)^2, \end{aligned}$$

(7)

and

$$\begin{aligned} (\textbf{1} \varvec{z}^\text {T} - k)^2. \end{aligned}$$

(8)

These transformations allow for the direct assimilation of the equality constraints into the objective function, facilitating an approximate resolution of the equations.

Furthermore, we implement the quadratic penalty method to address binary constraints, which enforces binary conditions without directly restricting the optimization variables to 0 or 1. The penalty term for the binary variable $z_n \in \{0,1\}$ is constructed as $z_n^2(1-z_n)^2$. If and only if $z_n = 0$ or $z_n = 1$ resulting in $z_n(1-z_n) = 0$, reflecting the binary requirement. Therefore, for the binary vector $\varvec{z} \in \{0,1\}^{1 \times N}$, the complete penalty term is formulated as

$$\begin{aligned} \varvec{z}(\varvec{1}-\varvec{z})^\text {T}(\varvec{1}-\varvec{z})\varvec{z}^\text {T}. \end{aligned}$$

(9)

The operational mechanism of the quadratic penalty method imparts a high cost for non-binary values of the variable. If $z_n$ is not strictly 0 or 1, the penalty term will cause an increase in the value of the objective function, which the optimization algorithm aims to minimize. Thus, the algorithm is driven to seek solutions that are as close to binary values as possible, in order to minimize the penalty term and consequently reduce the overall value of the objective function.

For the inequality constraints $0 \le w_n\le z_n$, we address them by the piecewise function, which can be described as follows:

$$\begin{aligned} \mathcal {P}(w_n, z_n) = {\left\{ \begin{array}{ll} -w_n,& \text {if }\, w_n<0\\ 0,& \text {if }\, 0\le w_n\le z_n\\ w_n-1& \text {if }\, z_n<w_n. \end{array}\right. } \end{aligned}$$

(10)

The formulation of (10) ensures that, even in cases of inequality constraint violations, the penalty added to the objective function remains always positive.

Based on the above analysis, we incorporate the penalty terms (7) to (10) into the minimization objective function, which can be defined as

$$\begin{aligned} \begin{aligned} \min _{\varvec{w},\varvec{z}} \mathbb {F}(\varvec{w},\varvec{z})&= \lambda \varvec{w} \hat{\varvec{\Sigma }} \varvec{w}^\text {T}- (1 - \lambda ) \varvec{w}{\varvec{\xi }}^\text {T} + \lambda _1((\varvec{1} + \varvec{c})\varvec{w}^\text {T} - 1)^2 + \lambda _2\left( \sum _{n\in [N]}\mathcal {P}(\varvec{w}, \varvec{z})\right) ^2\\&+ \lambda _3\varvec{z}(\varvec{1}-\varvec{z})^\text {T}(\varvec{1}-\varvec{z})\varvec{z}^\text {T}+\lambda _4(\varvec{1z}^\text {T} - k)^2 \end{aligned} \end{aligned}$$

(11)

The selection of penalty coefficients is crucial. Excessively high coefficients can lead to numerical difficulties and may overshadow other important aspects of the original objective function. Conversely, if they are too low, the penalty for violating binary constraints may be insufficient to prevent the optimizer from choosing non-binary values. Thus, during the problem-solving process, there may arise situations where the value of $z_n$ is non-binary while $w_n > z_n$, resulting in the penalty term $\mathcal {P}(x_n, z_n) < 0$. To avoid the impact of this occurrence on problem resolution, we square the second penalty term.

Nonlinear activated beetle antennae search improving egret swarm optimization algorithm

In this section, the introduction of a novel algorithm, named Nonlinear Activated Beetle Antennae Search Egret Swarm Optimization Algorithm (NBESOA), is presented. This algorithm integrates the strategies of NABAS and ESOA. The fundamental principles of ESOA and NABAS are initially outlined. Following this, the limitations inherent in ESOA are analyzed, and enhancements are proposed through the incorporation of NABAS strategies.

Basic egret swarm optimization algorithm

The ESOA process can be segmented into two distinct parts. The first part, encompassing the Sit-and-Wait and Aggressive strategies, demonstrates the cooperative prey-searching behaviour of an egret team within a solution space. Subsequently, the second part involves updating the search outcomes of each team, guided by specific discriminant conditions.

Searching strategy

In a team, each egret fulfills specific duties. Under the Sit-and-Wait strategy, Egret A adheres to a defined standard of behavior, which can be represented by an estimated tangent plane $\mathcal {A}(*)$, while the actual value of the objective function is culculated by $\mathbb {F}(*)$. Assume the position of the i-th egret in the team is ${\varvec{x}}_i \in \mathbb {R}^n$, where n is the dimension of this unresolved problem and this position carries a weight ${\varvec{\omega }}_i$ in the evaluation method. At the current position, the prey’s estimated value is parameterized as

$$\begin{aligned} {{\tilde{y}}}_i = \mathcal {A}({\varvec{x}}_i) = {\varvec{\omega }_i}{\varvec{x}}_i. \end{aligned}$$

However, Egret A’s judgment criteria have a deviation $\mathcal {E} _i = {\Vert {{{\tilde{y}}}_i - {y_i}} \Vert }^2 / 2$ from the actual value of the prey, where $y_i = \mathbb {F}({\varvec{x}}_i)$ is the value calculated by the objective function. To adjust this deviation, Egret A reorients in the direction ${\varvec{\tilde{d}}}_{i}$ guided by the practical gradient $\varvec{\tilde{g}}_i = {\partial {\mathcal {E} _i}}/{\partial {{\varvec{\omega }} _i}}$, which is defined as

$$\begin{aligned} {\varvec{\tilde{d}}}_{i} = {\varvec{\tilde{g}}_i} / {|| {\varvec{\tilde{g}}_i} ||}. \end{aligned}$$

(12)

Besides judging based on the current situation and adjusting the direction, Egret A also relies on the historical hunting experience of its team and the entire group. Assuming the team and the group currently have information about the optimal locations of prey ${\varvec{x}}_\text {hbest}$and ${\varvec{x}}_\text {gbest}$, the best fitness values $y_\text {hbest}$ and$y_\text {gbest}$, as well as the best correction directions ${\varvec{d}}_\text {hbest}$ and ${\varvec{d}}_\text {gbest}$. Based on the information from the team and the group, the direction corrections for Egret A at its current location can be calculated as follows

$$\begin{aligned} {\varvec{{\tilde{d}}}_{h,i}}= & \frac{({\varvec{x}}_\text {hbest} - {\varvec{x}}_i) \cdot (y_\text {hbest} - y_i)}{|| {{\varvec{x}}_\text {hbest}} - {\varvec{x}}_i ||^2} + {\varvec{d}}_\text {hbest}, \end{aligned}$$

(13)

$$\begin{aligned} {\varvec{{\tilde{d}}}_{g,i}}= & \frac{({\varvec{x}}_\text {gbest} - {\varvec{x}}_i) \cdot (y_\text {gbest} - y_i)}{|| {{\varvec{x}}_\text {gbest}} - {\varvec{x}}_i ||^2} + {\varvec{d}}_\text {gbest}, \end{aligned}$$

(14)

where, ${\varvec{{\tilde{d}}}_{h,i}}$ is the revised direction influenced by the team of Egret, while ${\varvec{{\tilde{d}}}_{g,i}}$ corresponds to the group. The combination of the (12) to (14) is represented as an integrated gradient, which is denoted as

$$\begin{aligned} {{\varvec{g}}_i} = ( 1 - {k_h} - {k_g} ) \cdot {\varvec{{\tilde{d}}}_i} + {k_h} \cdot {\varvec{{\tilde{d}}}_{h,i}} + {k_g} \cdot {\varvec{{\tilde{d}}}_{g,i}}, \end{aligned}$$

(15)

where $k_h \in [0,0.5)$ and $k_g \in [0,0.5)$. Thus, Egret A can move to the next position ${\varvec{x}}_{A,i}$ according to its judgement,

$$\begin{aligned} {\varvec{x}}_{A,i} = {\varvec{x}}_i + step_A \cdot \exp (-l / (-1 \cdot l_{\max })) \cdot h \cdot {{\varvec{g}}_i}, \end{aligned}$$

(16)

where $step_A \in (0,1]$ is the scalar quantity that controls the distance the Egret A moves, and h represents the gap between the up bound and with low bound. Additionally, l is the iteration count while $l_{\max }$ represents l gets maximum.

In the Aggressive strategy, Egret B freely conducts random searches throughout the entire solution space. This behavior is influenced by the random number $k_{B,i} \in (-\pi /2,\pi /2)$, which can be represented as

$$\begin{aligned} {\varvec{x}}_{B,i} = {\varvec{x}}_i + step_B \cdot {\tan ( k_{B,i} ) \cdot h} /(l+1). \end{aligned}$$

(17)

There is a factor $step_B \in (0,1]$ that controls the movement of Egret B. Unlike other members of the egret team, Egret B’s search for prey depends solely on itself.

As another aspect of the Aggressive strategy, Egret C appears to lack independent judgment. It prefers to pursue prey based on collaborative experience and adopts the encircling mechanism, which is described by

$$\begin{aligned} \begin{aligned} {\varvec{x}}_{C,i} = \,&( {1 - {k_m} - k_n} ) \cdot {\varvec{ x}_i} + {k_m} \cdot ({\varvec{x}}_\text {hbest} - {\varvec{x}}_i) + {k_n} \cdot ({\varvec{x}}_\text {gbest} - {\varvec{x}}_i), \end{aligned} \end{aligned}$$

(18)

where $k_n$ and $k_m$ are both random numbers in [0, 0.5).

Updating strategy

Egret A, Egret B, and Egret C provide their own opinions in (16)–(18) on team position updates, which can be combined into a solution matrix denoted to

$$\begin{aligned} {\varvec{x}}_{I,i} = [ {{\varvec{x}}_{A,i},{\varvec{x}}_{B,i},{\varvec{x}}_{C,i}} ]. \end{aligned}$$

(19)

Subsequently, according to (19), an optimal solution can be obtained:

$$\begin{aligned} {\varvec{y}}_{I,i} = [ {{y_{A,i}},{y_{B,i}},{y_{C,i}}} ]. \end{aligned}$$

(20)

Define $y_{min,i}$ as the minimum value of the total egret group in ${\varvec{y}}_{I,i}$ in the i-th iteration, the updated position can be determined by

$$\begin{aligned} {\varvec{x}}_{i+1} = \left\{ \begin{array}{l} {\varvec{x}}_{I,i}~~~~\text {if}~~y_{min,i}< y_i~~\text{or}~~r < 0.3\\ {{\varvec{x}}_i~~~~~~~~~~~~~~~~~~~~{\text {else}}}, \end{array} \right. \end{aligned}$$

(21)

with the random number $r \in (0,1)$, even if the Egret team does not find a better position in the ith iteration, it still has a $30\%$ chance of jumping out of the current position. The flowchart of ESOA is shown in Fig. 2.

Figure 2

Flowchart of the ESOA.

Nonlinear activated beetle antennae search algorithm

Unlike the egret group, which works in concert between individuals and the group during hunting, the BAS algorithm has only one particle in the search space, which relies entirely on individual searching ability. Each beetle is equipped with two antennae that hunt by collecting odour as a tool. Based on the comparative results collected from the antennae, the beetles decide their next location to move to. If the right antenna receives a higher concentration of odour than the left, it indicates that the food is on the right side, and vice versa. The search behavior of the left and right antennae for food is defined as follows,

$$\begin{aligned} {\varvec{x}_{R,i}} = {\varvec{x}_i} + \zeta _i \cdot {\varvec{b}} \textit{,} \quad {\varvec{x}_{L,i}} = {\varvec{x}_i} - \zeta _i \cdot {\varvec{b}}, \end{aligned}$$

where the right-side position $\varvec{x}_{R,i}$ and the left-side position $\varvec{x}_{L,i}$ are controlled by the length of antennae $\zeta _i$ and a random direction vector $\varvec{b}$. The concentration difference of food odour between the left and right position, represented as $\Delta \mathbb {F}$, influences the outcome of the signum function $\mathrm sgn(*)$. Furthermore, the beetle’s next step in the search space is given by

$$\begin{aligned} {\varvec{x}_{i+1}} = {\varvec{x}_i} \pm \psi _i \cdot {\varvec{b}} \cdot {\mathop {\textrm{sgn}}} ( \Delta \mathbb {F}) = {\varvec{x}_i} \pm \psi _i \cdot {\varvec{b}} \cdot {\mathop {\textrm{sgn}}}( \mathbb {F}({\varvec{x}_{R,i}}) - \mathbb {F}({\varvec{x}_{L,i}})), \end{aligned}$$

(22)

where $\lambda _i$ is the step factor controlling the convergence speed of BAS. The symbol ‘±’ appearing in (22) changes according to the type of optimization problem that BAS is solving. If BAS is applied to solve a minimization problem, ‘−’ should be used in (22), while ‘$+$’ is used for maximization problems.

After each iteration, both $\zeta$ and $\psi$ are updated to adapt to the gradually decreasing search area as the number of iterations increases. The specific update rules are as follows:

$$\begin{aligned} \begin{aligned}&\zeta _{i + 1} =0.95\zeta _i + 0.01,\\&\psi _{i + 1} = 0.95\psi _i. \end{aligned} \end{aligned}$$

(23)

However, this update rule may result in the BAS not effectively exploring the search space on certain gradient values, leading to premature convergence. To overcome this issue, a nonlinear activated factor $\mu$ is introduced into the BAS algorithm to control the update speed of the step size factors⁴⁴. The new update rule is

$$\begin{aligned} \begin{aligned}&\mu _{i+1} = \eta _i\psi _i\mu _i + (1-\eta _i)\mu _i,\\&\zeta _{i + 1} =\eta _i(0.95\zeta _i + 0.01)+(1-\eta _i)\zeta _i,\\&\psi _{i + 1} = 0.95 \psi _i \eta _i +(1-\eta _i)\psi _i, \end{aligned} \end{aligned}$$

(24)

where $\eta _i$ represents a decision factor that is influenced by the comparison of $\Delta \mathbb {F}$ and $\mu _i$. The definition of $\eta _i$ is

$$\begin{aligned} \eta _i = \left\{ \begin{array}{l} 1, \quad \text {if} ~~|\Delta \mathbb {F}| \le \mu _i\\ 0, \quad \text {else}. \end{array} \right. \end{aligned}$$

(25)

Under this rule, the particle that is far from the target continues to conduct wide-range searches, and only when it approaches the target within a certain range will lead $\zeta$ and $\psi$ to be updated.

NABAS strategy improving egret swarm optimization algorithm

Algorithm 1

Nonlinear activated beetle antennae search improving egret swarm optimization algorithm (NBESOA).

From the analysis of (12)–(18), it is revealed that, within ESOA, the philosophies of Egret A employing the Sit-and-Wait strategy and Egret B and C using the Aggressive strategy significantly diverge.

In (15), the determinants of Egret A’s positional update encompass three elements: the pseudo gradient of weight in the observation equation $\mathcal {A}(*)$, the team’s historical experience, and the group’s collective experience. The two factors based on historical experience make (15) the only part in ESOA influenced by the fitness function. However, in (15), the two stochastic numbers $k_h$ and $k_g$ can significantly impact the trajectory of Egret A, potentially leading to two extreme scenarios:

(1) When $k_h$ and $k_g$ both approach 0.5, Egret A may lose its own judgment, becoming entirely influenced by other members of the population, leading to premature convergence.

(2) In contrast, when both $k_h$ and $k_g$ asymptotically approach 0, Egret A’s behavior becomes exclusively reliant on its observational modality, precluding the team from optimizing actions based on fitness function outcomes, thereby resulting in a loss of directional focus.

Furthermore, while Egret B possesses a global perspective, potentially accruing enhanced benefits for the group, it concurrently incurs an increased energy expenditure. Conversely, the strategy of Egret C, predominantly influenced by historical experience, involves proximal circumnavigation and exploration, a method that is prone to entrap the group in local optima.

To address the aforementioned shortcomings of ESOA, a particle ${\varvec{x}}_{S,i}$ embedded with the NABAS strategy is introduced into the ESOA group. This particle conducts a fitness function search in the vicinity of its current position during each iteration, effectively resolving the issue where ESOA deviates from practical problems in extreme cases and reducing dependency on random numbers. Additionally, the introduction of an activation factor adaptively controls the update speed of the step size, and in comparison with Egret B, it reduces energy expenditure. Therefore, the updating strategies (19) and (20) of NBESOA are modified like below:

$$\begin{aligned} {\varvec{x}}_{I,i}= & [ {{\varvec{x}}_{A,i},{\varvec{x}}_{B,i},{\varvec{x}}_{C,i}},{\varvec{x}}_{S,i} ], \end{aligned}$$

(26)

$$\begin{aligned} {\varvec{y}}_{I,i}= & [ {y_{A,i}},{y_{B,i}},{y_{C,i}}, {y_{S,i}} ]. \end{aligned}$$

(27)

According to the best value in (27), NBESOA still updates the optimal position by (21). The pseudo code of NBESOA is shown in Algorithm 1.

Complexity analysis

For clarity of expression, we denote the maximum number of iterations in Algorithm 1 as K, and the population size of the NBESOA as M. Assuming that each statement in the NBESOA consumes one unit of time and that, apart from a single while loop for iteration, there are no loops within the functions “SITANDWAIT”, “AGGRESSIVE”, and “NABAS,” thus, these parts have a constant time complexity, denoted as O(1) . Consequently, the time complexity of the NBESOA is determined by the maximum number of iterations of the while loop, amounting to O(K) .

Regarding space complexity, it is necessary to account for all the data structures utilized within the algorithm. When the dimension of the optimization problem is N, the variables within NBESOA require storage for a matrix of dimensions $K \times N$ at maximum. Hence, the space complexity of the NBESOA is O(KN) .

Convergence performance of the improved ESOA

Four common test functions are selected to assess the convergence efficacy of NBESOA. These functions are Drop-wave, Schaffer N.2, Levy N.13, and Rastrigin, detailed in Table 3.

Table 3 Description of the test function.

Notably, each function is multimodal, non-convex, continuous, and possesses a singular global minimum within its solution space. To standardize the experimental results, we adjusted the original Drop-wave function by incrementing its cardinality by one, given its global optimum of 0. With their numerous local minima, these functions serve as an apt testbed for evaluating NBESOA’s proficiency in escaping local optima. We conducted 20 trials for each function using NBESOA, and the outcomes are presented in Fig. 3. Figure 3a illustrates the global convergence of NBESOA, demonstrating its rapid convergence to the optimal value within 200 iterations. Additionally, Fig. 3b displays a box plot of the 20 convergence outcomes, highlighting result variability. It is evident that NBESOA consistently converged to the global optimum in three of the functions across all trials, while the variance for the Levy N.13 function was within $10^{-9}$, indicating minimal fluctuation in the algorithm’s performance.

Figure 3

(a) Represents the fastest speed of convergence curve of NBESOA under the four functions. (b) It is a box plot of the results of 20 runs of NBESOA under four functions, showing the bias of the results.

Experimental results and discussion

This section will present a complete portfolio optimization process, covering stock selection, dataset analysis, and the MVPS-TCCC problem solved by the improved ESOA. Initially, based on the ChatGPT prompt framework proposed in “General frame of ChatGPT prompt for stock selection”, different indicators will be set for the three components of the framework (Strategy, Goal, and Constraint), creating multiple scenarios to input into ChatGPT and obtain corresponding stock groups. Subsequently, these stock groups will be thoroughly analyzed, from the overall composition to industry distribution, to explore the effectiveness of the framework. After finishing the analysis, one scenario will be selected for further refinement of investment objectives and construction of the required dataset, which will be used to solve the MVPS-TCCC problem solved by the improved ESOA. Additionally, to demonstrate the optimization effectiveness of the improved ESOA, it will also be compared with other optimization methods, highlighting its superiority.

Different cases of ChatGPT prompt for stock selection

In the above, a general ChatGPT prompt framework specifically designed for stock selection issues in the financial domain has been presented. To assess the efficacy of this framework, specifically how each part influences the process of selecting stocks for ChatGPT, we conducted experiments with various combinations of multiple indicators, and as shown in Fig. 4. Next, the selection process of indicators will be introduced.

Figure 4

An example diagram of the classification of key parts of the general framework for prompts.

Condition setting

In this framework, the “Strategy” part serves as a guideline where users can input their preferred investment strategies. Generally, professional investment managers often develop unique strategies based on their extensive knowledge and experience. In contrast, most non-professional investors may lack in-depth financial knowledge, leading to confusion and difficulties in their investment journey. ChatGPT, with its extensive knowledge base, not only answers basic financial questions but can also provide investment suggestions to inexperienced investors. In this paper, we selected three renowned investors: Warren Buffettt, Peter Lynch, and Benjamin Graham, to guide ChatGPT to emulate their thought patterns. Thus, when ChatGPT performs stock selection, it prioritizes the philosophies of these famous investors, offering non-professional investors an easy-to-understand and follow investment strategy.

Furthermore, each effective prompt must set a clear and specific “Goal” to define what users want to obtain from ChatGPT’s response. For the prompts that aim at stock selection, the fundamental goal is to have ChatGPT recommend a theoretical portfolio of stocks. At the same time, investors’ subjective requirements for this group of stocks can also be incorporated into the Goal. Therefore, in this paper, besides basic stock selection requirements, two additional goals related to stock returns were set, such as “outperforming the S&P 500 index” and “achieving rapid growth in the next six months”. To study the impact of these goals on the results generated by ChatGPT, it is incorporating them into specific portfolio optimization issues and comparing the corresponding outcomes is necessary.

“Constraint” indicates the objective limitations applied to stock portfolios. This paper focuses on two primary factors: Market Index (S&P 500 / NASDAQ) and Number Limit (15/30). The aim is to examine whether ChatGPT aligns with the unique characteristics of these indices in stock selection. Additionally, the study observes how variations in the number of stocks influence the overall characteristics of the portfolio.

Comparison for prompt cases under different constraints

In discussing the application of ChatGPT in stock selection, it is crucial to consider the impact of different strategies and constraints. Four cases were designed based on specific constraints to assess the performance of ChatGPT in stock selection under different strategies, as detailed in Table 4.

Table 4 Prompt cases under different constraints.

Figure 5

Components of the stocks selected by ChatGPT under Case 1 to Case 4.

The experimental design includes conducting five independent experiments for each case, using GPT-4 as the recommendation engine. In Cases 1 and 2, each experiment recommends 15 stocks, resulting in a total of 225 recommended stocks per case (3 strategies $\times$ 5 experiments $\times$ 15 stocks). For Cases 3 and 4, each experiment recommends 30 stocks, increasing the total to 450 stocks (3 strategies $\times$ 5 experiments $\times$ 30 stocks). To analyze this data in-depth, two types of chart methods are employed. First, the Venn Diagram of Fig. 5 is used to illustrate the intersections and differences in recommended stocks between different cases and strategies. Secondly, the industries involved in each experiment are recorded, and Fig. 6 is used to display the characteristics of industry distribution in different cases. The radar charts are based on the frequency of each industry’s appearance across the five experiments, thereby clearly revealing the tendencies of each strategy.

When analyzing the results of stock selection without the support of real-time financial data in Fig. 5, a notable trend observed is ChatGPT’s preference for selecting large and steadily developing companies. This trend reflects the common consideration of investors, that choosing such companies can significantly reduce investment risk, and it is also a primary factor considered by ChatGPT in stock selection. The Figures also reveal that although the set conditions were to construct portfolios of 15 and 30 stocks, the actual number of distinct stock codes in each case exceeded the specified amount. This phenomenon is partly due to randomness in ChatGPT’s qualitative analysis supported by non-financial data. For instance, well-established companies like Apple Inc. (AAPL) might be chosen repeatedly. However, some companies still show variability in ChatGPT’s analysis under the limitation of numbers. As the number of stocks increases, these companies tend to be included in the common selection of the three strategies. Further analysis of the figures shows some overlap in stock selection among the three investment strategies. Notably, the stocks chosen under Buffett’s strategy have a high degree of overlap with the other two strategies. As a student of Graham, Buffett’s investment strategy is heavily influenced by him. Building on this, he also tends to invest in quality companies with a sustained competitive advantage and clear growth prospects, aligning with Peter Lynch’s investment philosophy. This similarity in strategy is evident in different cases. Moreover, unique stock selections emerged under the strategies of Lynch and Graham. Lynch’s strategy is diverse, favoring investment in companies with high growth potential, while Graham focuses more on finding companies that are overlooked by the market but have solid fundamentals. This may be the reason that result in a large list of companies fitting Graham’s criteria.

Figure 6

Industry classification radar chart of ChatGPT-selected stock under Case 1 to Case 4.

In the details presented in Fig. 6, the industry preferences of different investment strategies, as well as the biases of various market indices, are distinctly evident. Figure 6a, b display stocks selected from the S&P 500 index, whereas Fig. 6c, d showcase those from the NASDAQ index. The differences in industry focus between these two indices are pronounced: NASDAQ’s involved industries are relatively fewer and predominantly centered around technology stocks, compared to the more diverse sectors covered by the S&P 500 index. In scenarios with 15 stocks selected from the S&P 500 index, the strategy of Graham shows a more significant advantage, reflecting his preference for lower-risk and more diversified investment portfolios. In contrast, Buffett’s strategy is more focused on certain specific industries, indicating a concentrated investment approach. Meanwhile, in situations with fewer stocks, primarily from the NASDAQ index, Lynch’s strategy demonstrates greater diversity. This is attributed to the typically better performance of growth stocks within the NASDAQ index. As the number of stocks increases to 30, Buffett’s strategy reveals its distinct superiority. Combining the advantages of the other two investors, Buffett’s approach excels regardless of the market type, showcasing its unique strengths in diverse market environments.

The above analysis indicates that simulating different investor roles to devise investment strategies is an effective approach for prompt. Although conducting stock selection analysis without real-time financial data support may not be as precise as analyses with financial data, ChatGPT can still effectively select stocks from various strategic perspectives.

Comparison for prompt cases under different goals

Table 5 Prompt cases under different goals.

Figure 7

Visualization of the selected stock portfolio characteristics under the three cases. (a–c) Represent all the stocks selected in Cases 4, Cases 5, and Cases 6 across five experiments, along with those ranking in the top 30 for mention frequency. (d–f) Display the covariance matrix heat maps for the top 30 stock combinations in Cases 5, Cases 6, and Cases 7, respectively.

In this section, we explore how altering the Goal parameter affects the stock selection performance of ChatGPT, with the specific categories listed in Table 5. The Strategy is set as Warren Buffett’s investment style, and the Constraint limits the selection to 30 stocks from the S&P 500 Index. Additionally, two further goals are set: “to exceed the S&P 500” and “to see a rapid appreciation in the next six months”. Considering the final training date for GPT-4 is April 2023, data from May 1, 2020, to April 30, 2023, was used for the training set, and data from May 1, 2023, to November 30, 2023, was used for the test set.

Firstly, ChatGPT was queried 10 times for each of the prompts relating to Cases 4 through 7, and all results were visualized in Table 7. It was observed that the total number of stocks generated exceeded the initial set of 30 for all three configurations. In Fig. 7a, Case 5, which had no additional goals, exhibited less randomness in the selection. In contrast, Fig. 7c, e show that the other two cases produced significantly more than 30 stocks. A heatmap analysis of the top 30 stocks from each case, as shown in Fig. 7b, indicated that Case 5 had the most uniform colour distribution, suggesting the lowest stock correlation under this scenario. The higher correlation observed in Fig. 7d for Case 6 and Fig. 7f for Case 7 may be attributed to the incorporation of goals aimed at increasing returns.

Historical stock data, sourced from the Yahoo Finance website⁴⁵, was utilized within the MVPS-TCCC model developed in this study. The model incorporated three distinct cardinality constraints and employed the NBESOA algorithm to determine the optimal solution. The optimal weights determined by the algorithm were used for a one-time purchase in the test dataset, with no further trading activities thereafter. The cumulative return curves displayed in Fig. 8 show the outcomes for all three cases. Analysis of these curves indicates that Case 7 exhibited higher cumulative returns over the observation period but also significant volatility, highlighting the high risk associated with high-return strategies. In contrast, Case 5’s cumulative return curve closely followed the S&P 500 index, indicating a lower-risk strategy unaffected by additional goals. Case 6 initially underperformed the S&P 500 index but showed the potential for long-term gains, outperforming the index as time progressed, despite possible underperformance during the strategy’s maturation phase.

Figure 8

Cumulative returns obtained by the NBESOA optimize the MVPS-TCCC problem with k = 30, 27 and 21.

Table 6 Parameters of NBESOA for the MVPS-TCCC problem.

The above analysis shows that ChatGPT’s stock recommendations displaying trends under different goal settings. However, the specificity of the goal statements significantly impacts the outcomes. For example, the “rapid growth in returns” goal mentioned in Case 7 is more explicitly stated than the “outperforming the S&P 500” goal in Case 6, which may account for the more pronounced advantage observed in Case 7’s results.

Algorithm comparison and discussion

In this section, we focus on the performance of improved optimization algorithms in the MVPS-TCCC problem, comparing NBESOA with GA, ESOA and Beetle Antennae Searching Egret Swarm Optimization Algorithm (BESOA). The experimental data was derived from the historical data of Case 7 stocks, covering the period from May 1, 2023, to November 30, 2023. k = 30, k = 27, and k = 21 were selected as the cardinality constraints for the MVPS-TCCC problem, examining the dynamic changes in investment portfolios under different cardinality constraints. To ensure the accuracy of our experiments, we conducted 10 trials under each constraint, and keep the same parameters in Table 6.

Table 7 Statistic results of portfolio optimization performed by four algorithms under Case 7.

Figure 9

Efficient frontier constructed from the dataset selected by Case 7. The color represents the algorithm and the pattern represents the difference of k. Overall, the portfolio constructed by NBESOA is closer to the ideal frontier.

Figure 10

Convergence performance of the four algorithms to solve the MVPS-TCCC problem when k is 30, 27 and 21. (a–c) Represent the convergence when the algorithms obtain the maximum Sharpe rate. (d–f) Represent the convergence of the loss function when the maximum Sharpe rate is obtained.

In Table 7, the statistic results of four algorithms are presented across metrics including risk, expected returns, Sharpe ratio, and overall constraints, detailed through maximum, minimum, and average values, as well as Schott’s spacing measure S. Notably, Schott’s spacing measure is specifically utilized to assess the uniform distribution of solutions along the Pareto front in multi-objective optimization, aiming to quantify the evenness of the spacing between solutions⁴⁶. It is evident that the improved NBESOA algorithm demonstrates exemplary performance in the Sharpe ratio under three distinct constraints while maintaining optimal overall constraints. In contrast, BESOA achieves better outcomes in maximizing average expected returns. Importantly, as the constraint level decreases to $k = 21$, the risk management capabilities of the other algorithms weaken, occasionally resulting in Sharpe ratios falling below zero. Nevertheless, NBESOA continues to maintain robust risk control, thereby sustaining a higher average Sharpe ratio. In terms of Schott’s spacing measure S, NBESOA consistently shows strong performance, indicating its capability to distribute solutions evenly across the solution space, which facilitates comprehensive exploration of viable investment portfolios. Additionally, we visualized the optimal investment portfolios of the four algorithms under different cardinality constraints on the efficient frontier. Figure 9 clearly shows that under the k = 30 constraint, NBESOA’s portfolio is closest to the efficient frontier. When the cardinality constraints is reduced to k = 27 and k = 21, NBESOA incurs less risk than other algorithms at the same level of expected return. In addition, different cardinality constraints affect the length of the efficient frontier.

On the other hand, we also presented the convergence curves of the Sharpe ratio and loss function for the four algorithms in Fig. 10. Among Fig. 10a–c, GA converges the fastest, but its performance in the Sharpe ratio is inferior to the others. NBESOA, with its activation factor, has expanded the search range, but this has slightly reduced its convergence speed, lower than the other algorithms which can be seen in Fig. 10d–f. Nevertheless, NBESOA maintains a higher Sharpe ratio than the other algorithms in all three scenarios. Overall, considering various indicators, NBESOA demonstrates the best comprehensive performance.

Conclusion

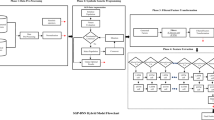
This paper delves into the domain of stock selection and asset allocation optimization within portfolio management. We introduced a structured Prompt framework specifically designed for stock selection, segmented into three components: Strategy, Goal, and Constraints. This structured approach facilitates an in-depth exploration of how variations in the prompt can influence the responses of the generative AI tools. Utilizing roles to represent specific strategies enables non-professional investors to navigate investments more simply. The Goal and Constraints components reflect the investor’s intentions from subjective and objective perspectives, respectively, making this framework highly adaptable for investors at all levels. Through the construction of seven distinct cases, analyzing aspects such as stock selection and their recommendation frequency, industry distribution, risk covariance matrix, and cumulative returns, we observed that the three components of the framework significantly influence stock recommendations. It was also noted that when issuing instructions incorporating subjective factors to the generative AI tools, clarity and specificity are paramount.

Furthermore, a variant of the ESOA algorithm that integrates the NABAS strategy was proposed, which is termed NBESOA. The incorporation of NABAS enhances the sensitivity of ESOA to the loss function and expands the algorithm’s search area. This improved algorithm is applied to solve the MVPS-TCCC problem, addressing both risk minimization and return maximization. The performance of NBESOA is compared against GA, ESOA, and BESOA algorithms. Results indicate that NBESOA is capable of achieving higher Sharpe ratios with lower risk, demonstrating superior comprehensive performance in optimizing the MVPS-TCCC problem. However, the introduction of the activation factor to expand the search range has slowed the convergence speed of the algorithm and increased computational costs to some extent. Future work will continue to address this issue to further enhance its performance. It is crucial to emphasize that now the stock recommendations generated by AI tools are based on their understanding of training data and do not possess real-time market analysis capabilities. Therefore, a comprehensive analysis of the latest market data and trends is essential before making actual investments. How to effectively integrate AI tools with real-time financial data is also significant.